Cho hình chóp S.ABCD có đáy là hình bình hành ABCD. Gọi G là trọng tâm của tam giác SAB và I là trung điểm của AB. Lấy điểm M trong đoạn AD sao cho AD = 3AM.

a) Tìm giao tuyến của hai mặt phẳng (SAD) và (SBC).

b) Đường thẳng qua M song song với AB cắt CI tại N.

Chứng minh rằng NG // (SCD).

c) Chứng minh rằng MG // (SCD).

Lời giải

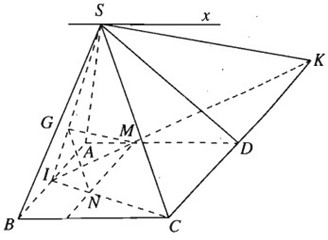
a) Dễ thấy S là một điểm chung của hai mặt phẳng (SAD) và (SBC).

Ta có: \[\left\{ \begin{array}{l}AD \subset (SAD)\\BC \subset (SBC)\\AD\parallel BC\end{array} \right.\]

Do đó (SAD) ∩ (SBC) = Sx và Sx // AD // BC.

b) Ta có: MN // IA // CD

Suy ra \[\frac{{AM}}{{AD}} = \frac{{IN}}{{IC}} = \frac{1}{3}\].

Mà \[\frac{{IG}}{{IS}} = \frac{1}{3}\] (G là trọng tâm của ∆SAB) nên \[\frac{{IG}}{{IS}} = \frac{{IN}}{{IC}} = \frac{1}{3}\].

Ta có SC ⊂ (SCD) suy ra GN // (SCD).

c) Giả sử IM cắt CD tại K nên SK ⊂ (SCD).

MN // CD ⇒ \[\frac{{MN}}{{CK}} = \frac{{IN}}{{IC}} = \frac{1}{3}\] ⇒ \[\frac{{IM}}{{IK}} = \frac{1}{3}\].