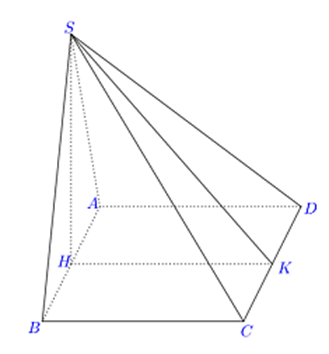
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, tam giác SAB
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, tam giác SAB cân tại S và nằm trong mạt phẳng vuông góc với mặt phẳng (ABCD). Góc giữa hai mặt phẳng (SCD) và (ABCD) là 60°. Tính thể tích của khối chóp S.ABCD.