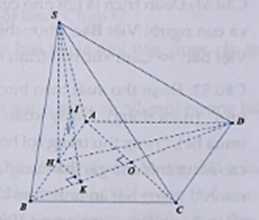
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, sd = 3a/2, hình chiếu vuông góc của s trên mặt phẳng (ABCD) là trung điểm của cạnh AB
44
10/08/2024
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SD=3a2, hình chiếu vuông góc của s trên mặt phẳng (ABCD) là trung điểm của cạnh AB. Biết khoàng cách từ A đến mặt phẳng (SBD) là mna, với mn là phân số tối giản. Tính m + n.
Trả lời
Đáp án: 5
Gọi H là trung điểm của AB, O là giao điểm của AC và BD.
Theo đề bài ta có SH⊥(ABCD).
ΔHAD vuông tại A có HD=√AH2+AD2=√a24+a2=a√52.
ΔSHD vuông tại H có SH=√SD2−HD2=√9a24−5a24=a.
Dựng HK⊥BD,(K∈BD).
Có BD⊥HK và BD⊥SH⇒BD⊥(SHK) mà BD⊂(SBD)⇒(SBD)⊥(SHK) hai mặt phẳng này vuông góc với nhau theo giao tuyến SK, dựng HI⊥SK,(I∈SK)⇒HI⊥(SBD).
Vậy d(H,(SBD))=HI.
Ta có HK=12AO=a√24, trong ΔSHK có 1HI2=1HK2+1HS2=8a2+1a2=9a2⇒HI=a3.
Hai điểm A và H nằm trên đường thẳng có giao điểm với mp (SBD) tại B có:
d(A,(SBD))d(H,(SBD))=ABHB=2⇒d(A,(SBD))=2
Như vậy
.