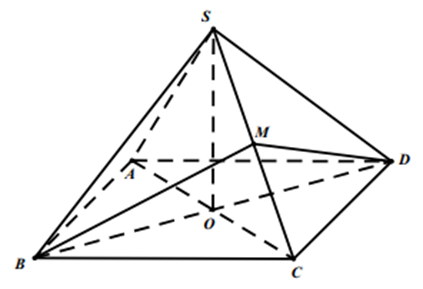
Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O, đường thẳng SO vuông góc với mặt phẳng (ABCD). Biết $\text{BC}=\text{SB}=\text{a},\text{SO}=\frac{\text{a}\sqrt{6}}{3}$ . Số đo của góc giữa hai mặt phẳng (SBC) và (SCD) là bao nhiêu độ?

Gọi M là trung điểm của SC, do tam giác SBC cân tại B nên ta có $\text{SC}\perp \text{BM}$.Theo giả thiết ta có $\text{BD}\perp \left(\text{SAC}\right)\Rightarrow \text{SC}\perp \text{BD}$.

Do đó $\text{SC}\perp \left(\text{BCM}\right)$ suy ra $\text{SC}\perp \text{DM}$.Từ và suy ra góc giữa hai mặt phẳng (SBC) và (SCD) là góc giữa hai đường thẳng BM và DM.

Ta có $\Delta \text{SBO}=\Delta \text{CBO}$ suy ra $\text{SO}=\text{CO}=\frac{\text{a}\sqrt{6}}{3}$. Do đó $\text{OM}=\frac{1}{2}\text{SC}=\frac{\text{a}\sqrt{3}}{3}$.