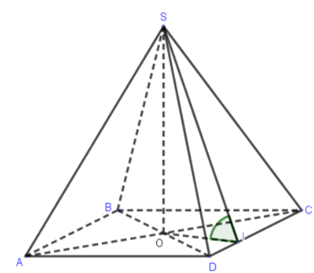
Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O, AB = a, góc BAD = 60 độ
\({S_{ABC{\rm{D}}}} = 2{S_{ABD}} = AB.AD.\sin \widehat {BAD} = a.a.\sin 60^\circ = \frac{{{a^2}\sqrt 3 }}{2}\)
Trong (ABCD), dựng OI ⊥ CD
Ta có \(\left. {\begin{array}{*{20}{c}}{CD \bot OI}\\{CD \bot SO}\end{array}} \right\} \Rightarrow CD \bot \left( {SOI} \right) \Rightarrow CD \bot SI\)
Do đó, ((SCD); (ABCD)) = (SI; OI) = \(\widehat {SIO} = 60^\circ \)
∆OCI vuông tại I nên
\(\sin \widehat {OCI} = \frac{{OI}}{{OC}} \Leftrightarrow OI = OC.\sin \widehat {OCI} = \frac{{a\sqrt 3 }}{2}.\sin 30^\circ = \frac{{a\sqrt 3 }}{4}\)
∆SOI vuông tại O nên
\(\tan \widehat {SIO} = \frac{{SO}}{{OI}} \Rightarrow SO = OI.\tan \widehat {SIO} = \frac{{a\sqrt 3 }}{4}.\tan 60^\circ = \frac{{3a}}{4}\)
Vậy \({V_{S.ABCD}} = \frac{1}{3}{S_{ABCD}}.SO = \frac{1}{3}.\frac{{{a^2}\sqrt 3 }}{2}.\frac{{3a}}{4} = \frac{{{a^3}\sqrt 3 }}{8}\)