Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm I, cạnh a, góc BAD
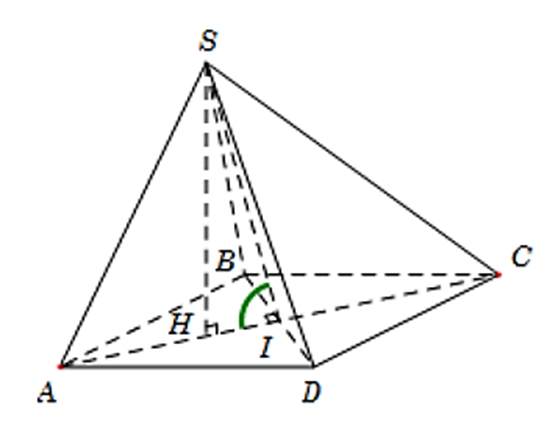
Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm I, cạnh a, ^BAD=60∘, SA=SB=SD=a√32. Gọi α là góc giữa hai mặt phẳng (SBD) và (ABCD). Mệnh đề nào sau đấy đúng?
A. tanα=√5.
B. tanα=√55.
C. tanα=√32.
D. α=45∘.