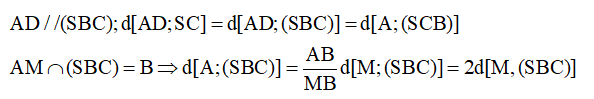Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a và AC =a. Biết tam giác SAB cân tại S và nằm trong mặt phẳng vuông góc với mặt đáy.

Trả lời

Gọi M trung điểm AB nên $SM\perp \left(ABCD\right)$.

Dựng $ME\perp BC;MF\perp SE\Rightarrow d[M,(SBC\left)\right]=MF$

$ME=\frac{1}{2}\cdot \frac{a\sqrt{3}}{2}=\frac{a\sqrt{3}}{4}$ (phân nữa đường cao tam giác đều ABCMD là hình chiếu SD lên mặt phẳng (ABCD) nên $(SD,\widehat{\left(ABCD\right)})=\widehat{SDM}$

$\begin{array}{l}M{D}^2=A{M}^2+A{D}^2-2AM.AD.\cos \widehat{MAD}\\ =\frac{a^2}{4}+a^2-2.\frac{a}{2}.a.\cos {120}^{°}=\frac{7a^2}{4}.d\end{array}$

$SM=DM.tan\widehat{SDM}=\frac{a\sqrt{7}}{2}\cdot \sqrt{3}=\frac{a\sqrt{21}}{2}$

$\frac{1}{M{F}^2}=\frac{1}{M{S}^2}+\frac{1}{M{E}^2}=\frac{4}{21a^2}+\frac{16}{3a^2}=\frac{116}{21a^2}$

$d[AD,SC]=2MF=\frac{a\sqrt{609}}{29}\text{. }$

Vậy $p-q=609-29=580$