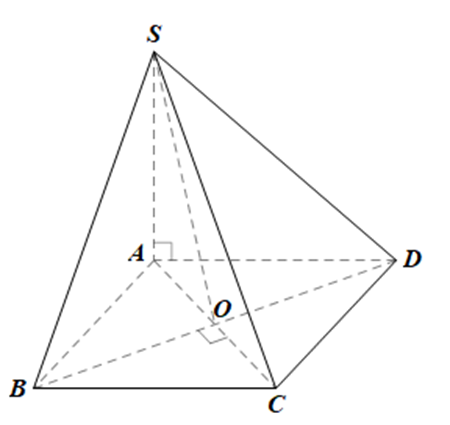
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, góc ABC = 60 độ
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, \(\widehat {ABC} = {\rm{ }}60^\circ ,\;\) cạnh bên \(SB = a\sqrt 2 \) và SA vuông góc với ABCD. Tính góc giữa SB và (SAC).
A. 90°;
B. 30°;
C. 45°;
D. 60°.