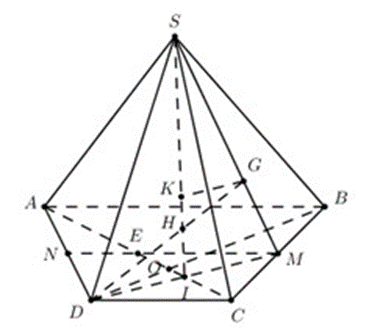
Cho hình chóp S.ABCD có đáy ABCD là hình thang với AB // CD và AB = 2DC. Gọi O là giao điểm của AC và BD, G là trọng tâm tam giác SBC, H là giao điểm của DG và (SAC). Tính tỉ số \[\frac{{GH}}{{GD}}\].
Gọi M là trung điểm của BC, I = AC ∩ DM .
Trong (SDM) gọi H = DG ∩ SI ta có:
• I ∈ AC ⇒ I ∈ (SAC) ⇒ SI ⊂ SAC
• H ∈ SI ⇒ H ∈ (SAC) ⇒ H = DG ∩ (SAC).
Gọi N là trung điểm của AD, E = AC ∩ MN
Nên MN là đường trung bình của hình thang ABCD
\[ \Rightarrow MN = \frac{{AB + CD}}{2} = \frac{{2CD + CD}}{2} = \frac{{3CD}}{2}\]
Áp dụng định lí Ta-lét, ta có:
• \[\frac{{NE}}{{CD}} = \frac{{AN}}{{AD}} = \frac{1}{2} \Rightarrow NE = \frac{1}{2}CD \Rightarrow ME = \frac{3}{2}CD - \frac{1}{2}CD = CD\]
• \[\frac{{IM}}{{ID}} = \frac{{CD}}{{MN}} = \frac{{ME}}{{CD}} = 1 \Rightarrow IM = ID\]
Kẻ GK // DM, áp dụng định lí Vi-ét ta có:
\[\frac{{GH}}{{DH}} = \frac{{KG}}{{ID}} = \frac{{KG}}{{IM}} = \frac{{KG}}{{IM}} = \frac{{SG}}{{SM}} = \frac{2}{3}\]
\[ \Rightarrow \frac{{GH}}{{GH + DH}} = \frac{2}{{2 + 3}} = \frac{2}{5} \Rightarrow \frac{{GH}}{{GD}} = \frac{2}{5}\].