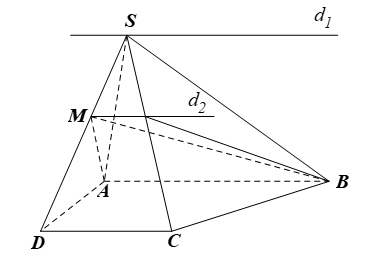
Cho hình chóp S.ABCD có đáy ABCD là hình thang, đáy lớn AB. Gọi M là điểm bất kì thuộc đoạn thẳng SD. a) Tìm các giao tuyến: d1 = (SAB) ∩ (SCD); d2 = (SCD) ∩ (MAB). b) Chứng minh d1 // d2.
Cho hình chóp S.ABCD có đáy ABCD là hình thang, đáy lớn AB. Gọi M là điểm bất kì thuộc đoạn thẳng SD.
a) Tìm các giao tuyến: d1 = (SAB) ∩ (SCD); d2 = (SCD) ∩ (MAB).
b) Chứng minh d1 // d2.