Cho hình chóp S.ABCD có đáy ABCD là hình thang (AB // CD). Gọi M là trung điểm của đoạn thẳng SD (H.4.28). a) Xác định giao tuyến của mặt phẳng (MAB) và (SCD). b) Gọi N là giao điểm của đườ
29
25/07/2024
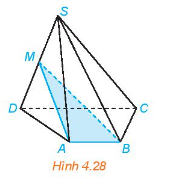
Cho hình chóp S.ABCD có đáy ABCD là hình thang (AB // CD). Gọi M là trung điểm của đoạn thẳng SD (H.4.28).
a) Xác định giao tuyến của mặt phẳng (MAB) và (SCD).
b) Gọi N là giao điểm của đường thẳng SC và mặt phẳng (MAB). Chứng minh rằng MN là đường trung bình của tam giác SCD.
Trả lời
Lời giải:
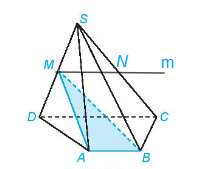
a) Vì M thuộc SD nằm trong mặt phẳng (SCD) nên M thuộc mặt phẳng (SCD).
Mà M thuộc mặt phẳng (MAB) nên M là điểm chung của hai mặt phẳng (MAB) và (SCD).
Lại có hai mặt phẳng (MAB) và (SCD) chứa hai đường thẳng song song AB và CD.
Do đó, giao tuyến của hai mặt phẳng (MAB) và (SCD) là đường thẳng m đi qua M và song song với AB, CD.
b) Trong tam giác SCD, đường thẳng m đi qua điểm M và song song với CD cắt cạnh SC tại một điểm N.
Vì N thuộc m và m nằm trong mặt phẳng (MAB) nên N thuộc mặt phẳng (MAB).
Vậy N là giao điểm của đường thẳng SC và mặt phẳng (MAB).
Xét tam giác SCD có M là trung điểm của SD, MN // CD và N thuộc SC nên đường thẳng MN là đường trung bình của tam giác SCD.


