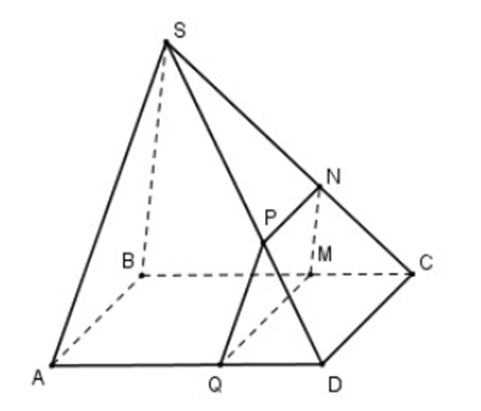
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N, P, Q lần lượt là các điểm nằm trên các cạnh BC, SC, SD, AD sao cho MN // BS, NP // CD, MQ // CD. Hỏi PQ song song với mặt phẳng nào sau đây?
A. mp(SBC);
B. mp(SAB);
C. mp(SAD);
D. mp(SCD).
Đáp án đúng là: B
Vì MN // BS nên \(\frac{{CN}}{{CS}} = \frac{{CM}}{{CB}}\) (định lí Ta – let)
Vì MQ // CD // AB nên \(\frac{{CM}}{{CB}} = \frac{{DQ}}{{DA}}\)
Vì PN // CD nên \(\frac{{CN}}{{CS}} = \frac{{PD}}{{D{\rm{S}}}}\) (định lí Ta – let)
Suy ra \(\frac{{DQ}}{{DA}} = \frac{{PD}}{{D{\rm{S}}}}\)
Do đó PQ // SA (định lí Ta – let đảo)
Ta có SA ⊂ (SAB), SA ⊂ (SAD)
Mà PQ ⊂ (SAD)
Suy ra PQ // (SAB), PQ không song song với mặt phẳng(SAD)
Vậy ra chọn đáp án B.