Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N lần lượt là trung điểm của hai cạnh AB và CD, P là trung điểm của SA. Chứng minh: a) MN song song với các mặt phẳng (SBC) và (SAD)
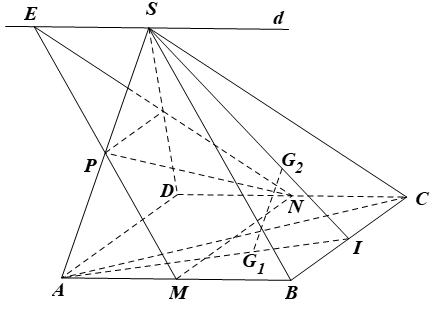
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N lần lượt là trung điểm của hai cạnh AB và CD, P là trung điểm của SA. Chứng minh:
a) MN song song với các mặt phẳng (SBC) và (SAD);
b) SB song song với (MNP);
c) SC song song với (MNP).
d) Gọi G1 và G2 theo thứ tự là trọng tâm của hai tam giác ABC và SBC. Chứng minh G1G2 song song với (SAD).