Cho hình chóp S.ABCD, có đáy ABCD là hình bình hành. Gọi M, N lần lượt là trung điểm của AB và SC. Tìm giao tuyến của (SMN) và (SBD).

Trả lời

Lời giải

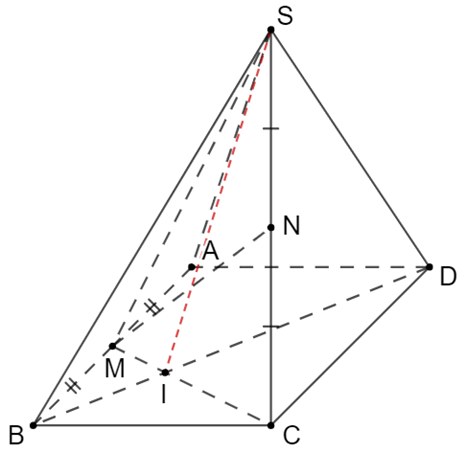
Ta có: \(M \in SM,\;N \in SC\) và SM cắt SC tại S \( \Rightarrow MN \in \left( {SMC} \right)\).

Gọi I là giao điểm của BD và MC \( \Rightarrow I \in \left( {SMC} \right)\)

Vì \(I \in BD,\;BD \in \left( {SBD} \right)\) nên \(I \in \left( {SBD} \right)\)

Ta thấy: (SBD) và (SMC) có điểm chung là S

Þ SI là giao tuyến của (SBD) và (SMC)

Þ SI giao tuyến của (SBD) và (SMN).