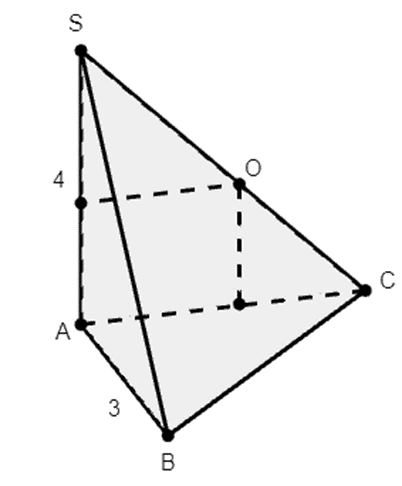
Cho hình chóp S.ABCD có đáy ABC là tam giác vuông cân tại B, cạnh AB = 3. Cạnh bên SA = 4 và vuông góc với mặt phẳng đáy. Tính bán kính mặt cầu ngoại tiếp hình chóp S.ABCD.

A. \(\sqrt {34} \);

B. 6;

C. \(\frac{{\sqrt {34} }}{2}\);

D. \(2\sqrt 3 \).

Đáp án đúng là: C

Gọi O là trung điểm của SC.

Khi đó O là tâm mặt cầu ngoại tiếp hình chóp S.ABC.

Ta có: AC² = 3² + 3² = 18; SC² = SA² + AC² = 4² + 18 = 34

Bán kính mặt cầu ngoại tiếp hình chóp S.ABC là: \(R = \frac{{SC}}{2} = \frac{{\sqrt {34} }}{2}\).