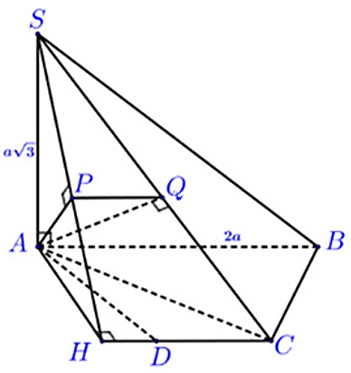
Ta có ABCD là nửa lục giác đều suy ra AD = DC = CB = a

Dựng đường thẳng đi qua điểm A và vuông góc với mặt phẳng (SCD)

Trong (ABCD) dựng AH ^ CD tại H suy ra CD ^ (SAH)

Trong (SAH) dựng AP ^ SH Þ CD ^ AP Þ AP ^ (SCD)

Tiếp tục dựng đường thẳng đi qua A và vuông góc với mặt phẳng (SBC)

Trong (SAC) dựng đường AQ ^ SC

Vì BC ^ AC, BC ^ SA Þ BC ^ (SAC) Þ BC ^ AQ

Þ AQ ^ SBC)

Do đó góc giữa hai mặt phẳng (SBC), (SCD) là góc giữa hai đường thẳng vuông góc lần lượt với hai mặt phẳng là AP và AQ.

Ta có: ∆SAC vuông cân tại A suy ra \(AQ = \frac{{SC}}{2} = \frac{{a\sqrt 6 }}{2}\)

Mặt khác ∆AQP vuông tại O suy ra

\(\cos \widehat {PAQ} = \frac{{AP}}{{AQ}} = \frac{{\sqrt {10} }}{5} \Rightarrow \widehat {PAQ} = \arccos \frac{{\sqrt {10} }}{5}\).