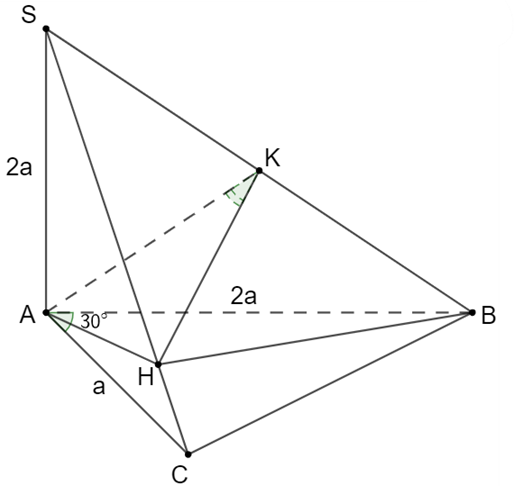
Cho hình chóp S.ABC có đường cao SA = 2a, tam giác ABC vuông ở C có AB = 2a, $\widehat{CAB}=30°$. Gọi H là hình chiếu vuông của A trên SC. Tính theo a thể tích của khối chóp H.ABC. Tính cosin của góc giữa hai mặt phẳng (SAB), (SBC).

Trong mặt phẳng (SAC), kẻ HI // SA thì HI $\perp$ (ABC).

Ta có: $CA=AB.\cos 30°=a\sqrt{3}$

Do đó: $S_{ABC}=\frac{1}{2}AB.AC.\sin 30°=\frac{1}{2}.2a.a\sqrt{3}.\sin 30°=\frac{a^2\sqrt{3}}{2}$

Ta có: $\frac{HI}{SA}=\frac{HC}{SC}=\frac{HC.SC}{S{C}^2}=\frac{A{C}^2}{S{C}^2}$

$$\begin{gathered} =\frac{A{C}^2}{S{A}^2+A{C}^2}=\frac{3a^2}{4a^2+3a^2}=\frac{3}{7} \\ \Rightarrow HI=\frac{6}{7}a \end{gathered}$$

Vậy $V_{H.ABC}=\frac{1}{3}{S}_{ABC}.HI=\frac{1}{3}.\frac{a^2\sqrt{3}}{2}.\frac{6}{7}a=\frac{a^3\sqrt{3}}{7}$

Gọi K là hình chiếu vuông góc của A lên SB. Ta có:

AH $\perp$ SC, AH $\perp$ CB (Do CB $\perp$ (SAC)).

=> AH $\perp$ (SBC) => AH $\perp$ SB

Lại có: SB $\perp$ AK => SB $\perp$ (AHK).

Do đó, góc giữa hai mặt phẳng (SAB), (SBC) là  $\widehat{HKA}$