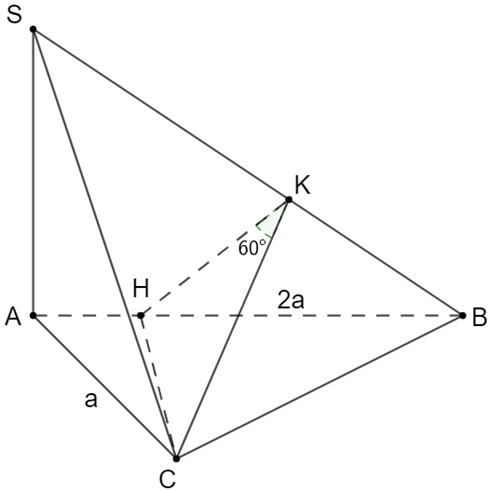
Cho hình chóp S.ABC có đáy là tam giác ABC vuông tại C, AB  2a, AC  a và SA vuông góc với mặt phẳng (ABC).

Trả lời

Trong ∆ABC kẻ CH $\perp$ AB

Mà SA $\perp$ CH (SA $\perp$ (SAB))

=> CH $\perp$ (SAB) => CH $\perp$ SB (1)

$$\begin{gathered} BC=\sqrt{A{B}^2-A{C}^2}=a\sqrt{3} \\ BH.BA=B{C}^2\Rightarrow BH=\frac{3a}{2} \\ CH=\sqrt{B{C}^2-B{H}^2}=\frac{\sqrt{3}}{2}a \end{gathered}$$

Trong ∆SAB kẻ HK $\perp$ SB (2)

Từ (1) và (2) => SB $\perp$ (HKC)

=> SB $\perp$ KC

Góc giữa hai mặt phẳng (SAB) và (SBC) là $\widehat{CKH}=60°$

Trong tam giác vuông CKH có:

$$\begin{gathered} HK=CH.\cot 60°=\frac{1}{2}a \\ BK=\sqrt{B{H}^2-H{K}^2}=a\sqrt{2} \end{gathered}$$

Xét ∆SAB và ∆HKB có:

$\widehat{SAB}=\widehat{HKB}=90°$

$\widehat{B}$ : góc chung

=> ∆SAB ᔕ ∆HKB (g.g)

$\Rightarrow \frac{SA}{HK}=\frac{AB}{BK}=\frac{2a}{a\sqrt{2}}\Rightarrow SA=\frac{a}{\sqrt{2}}$

Thể tích của khối chóp S.ABC là:

$V=\frac{1}{3}SA.S_{ABC}=\frac{1}{3}\cdot \frac{a}{\sqrt{2}}\cdot \frac{1}{2}\cdot a\sqrt{3}\cdot a=\frac{a^3\sqrt{6}}{12}$

Tam giác HKA vuông tại H (vì AH $\perp$ (SBC), HK $\subset$(SBC))

$\sin \widehat{HKA}=\frac{AH}{AK}=\frac{\frac{2a\sqrt{3}}{\sqrt{7}}}{a\sqrt{2}}=\frac{\sqrt{6}}{\sqrt{7}}\Rightarrow \cos \widehat{HKA}=\frac{\sqrt{7}}{7}$