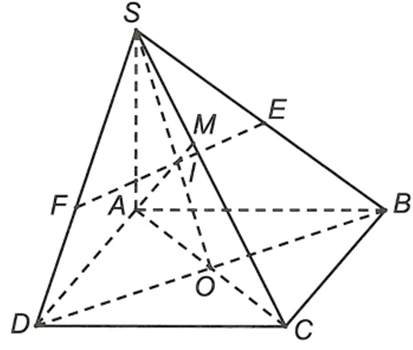
Cho hình chóp S.ABC có đáy là hình vuông cạnh a, SA = a căn bậc hai 2 và vuông góc với mặt phẳng (ABCD). Gọi M là trung điểm cạnh SC.
Cho hình chóp S.ABC có đáy là hình vuông cạnh a, và vuông góc với mặt phẳng (ABCD). Gọi M là trung điểm cạnh SC. Mặt phẳng qua A và M đồng thời song song với đường thẳng BD cắt SB, SD lần lượt tại E, F. Bán kính mặt cầu đi qua 5 điểm S, A, E, M, F nhận giá trị nào sau đây?
A. a
B.
C.
D.