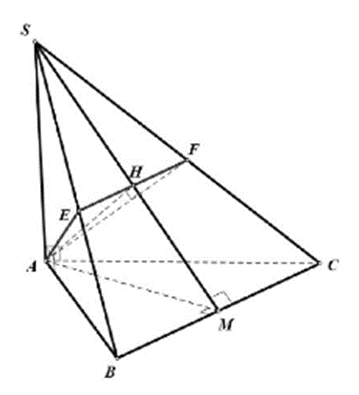
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, SA vuông góc với mặt đáy. Gọi M là trung điểm BC. Mặt phẳng (P) đi qua A và vuông góc với SM cắt SB, SC lần lượt tại E, F.

A. $V=\frac{a^3}{2}$

B. $V=\frac{a^3}{8}$

C. $\text{V}=\frac{2{\text{a}}^3}{5}$

D. $V=\frac{a^3}{12}$

Trả lời

Ta có $BC\perp SM$. Gọi H là hình chiếu vuông góc của A trên SM .

Do $\text{FE}=\left(\text{P}\right)\cap \left(\text{SBC}\right)\Rightarrow \text{FE}\perp \text{SM}\Rightarrow \text{FE}//\text{BC}$ và  đi qua H.

${\text{V}}_{\text{S}.\text{AEF}}=\frac{1}{4} {\text{V}}_{\text{S}.\text{ABC}}\iff \frac{\text{SE}}{\text{SB}}\cdot \frac{\text{SF}}{\text{SC}}=\frac{1}{4}\iff {\left(\frac{\text{SH}}{\text{SM}}\right)}^2=\frac{1}{4}\Rightarrow \frac{\text{SH}}{\text{SM}}=\frac{1}{2}$

Vậy H là trung điểm cạnh SM . Suy ra $△\text{SAM}$ vuông cân tại A

$\Rightarrow \text{SA}=\frac{\text{a}\sqrt{3}}{2}$. Vậy ${\text{V}}_{\text{SABC}}=\frac{1}{3}\cdot \frac{\text{a}\sqrt{3}}{2}\cdot \frac{{\text{a}}^2\sqrt{3}}{4}=\frac{{\text{a}}^3}{8}$.