Lời giải
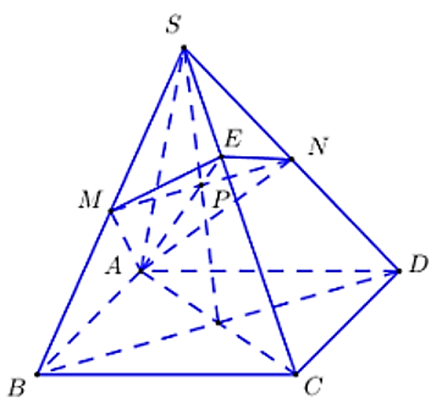
Gọi O là tâm đáy và P là trung điểm của MN.
Suy ra I cũng là trung điểm của SO (theo định lí Ta-lét).
Trong tam giác SAC, nối AP cắt SC tại E.
Áp dụng Menelaus cho tam giác SPC có ba điểm thẳng hàng là A, P, E ta có:
\(\frac{{SE}}{{EC}}.\frac{{CA}}{{AO}}.\frac{{OP}}{{SP}} = 1 \Leftrightarrow \frac{{SE}}{{EC}}\,.\,2\,.\,1 = 1\)
\( \Leftrightarrow SE = \frac{1}{2}EC \Leftrightarrow SE = \frac{1}{3}SC\).
Do S.ABCD là chóp đều \( \Rightarrow \left\{ \begin{array}{l}{V_{S.AMEN}} = 2{V_{S.ANE}}\\{V_{S.ABCD}} = 2{V_{S.ACD}}\end{array} \right.\)
\( \Rightarrow \frac{{{V_{S.AMEN}}}}{{{V_{S.ABCD}}}} = \frac{{{V_{S.ANE}}}}{{{V_{S.ACD}}}} = \frac{{SA}}{{SA}}.\frac{{SN}}{{SD}}.\frac{{SE}}{{SC}} = 1.\frac{1}{2}.\frac{1}{3} = \frac{1}{6}\) (Theo định lí Simsons).