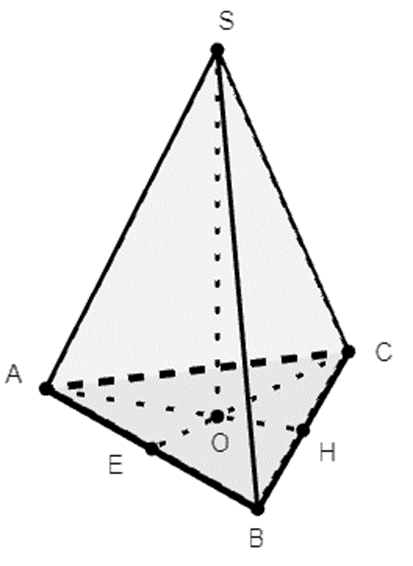
Gọi O là tâm của tam giác ABC

Suy ra \(SO \bot SABC\) (do SABC đều)

Khi đó góc hợp giữa SC và (ABC) là góc: \(\widehat {SCO} = 60^\circ \)

Xét ∆SOC vuông tại A.

\(SO = \sin 60^\circ .SC = \frac{{\sqrt 3 }}{2}a\)

\(OC = \cos 60^\circ .SC = \frac{1}{2}a\)

\( \Rightarrow CE = \frac{3}{2}OC = \frac{3}{4}a\) (tính chất của đường trung tuyến tam giác đều)

\( \Rightarrow AB = \frac{2}{{\sqrt 3 }}.CE = \frac{{2\sqrt 3 }}{4}a = \frac{{\sqrt 3 }}{2}a\)

\( \Rightarrow {V_{SABC}} = \frac{1}{3}.SO.{S_{ABC}} = \frac{1}{3}.\frac{{\sqrt 3 }}{2}a.\frac{1}{2}.\frac{3}{4}a.\frac{{\sqrt 3 }}{2}a = \frac{{3{a^3}}}{{32}}\).