Cho hình bình hành ABCD, gọi O là giao điểm của AC và BD. Các khẳng định sau đúng hay sai?

a) $\left| {\overrightarrow {AB} + \overrightarrow {AD} } \right| = \left| {\overrightarrow {AC} } \right|;$

b) $\overrightarrow {AB} + \overrightarrow {BD} = \overrightarrow {CB} ;$

c) $\overrightarrow {OA} + \overrightarrow {OB} = \overrightarrow {OC} + \overrightarrow {OD} .$

Lời giải

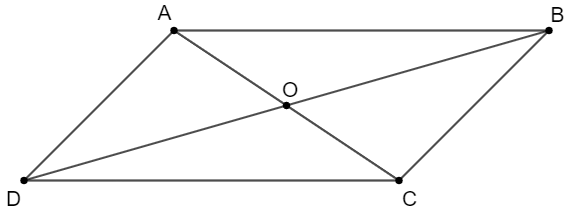
+ Do ABCD là hình bình hành nên $\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC}$.

Do đó: $\left| {\overrightarrow {AB} + \overrightarrow {AD} } \right| = \left| {\overrightarrow {AC} } \right|$.

Vậy khẳng định a) đúng.

+ Ta có: $\overrightarrow {AB} + \overrightarrow {BD} = \overrightarrow {AD}$

Mà $\overrightarrow {AD} = \overrightarrow {BC}$ (Do ABCD là hình bình hành)

Do đó: $\overrightarrow {AB} + \overrightarrow {BD} = \overrightarrow {AD} = \overrightarrow {BC} = - \overrightarrow {CB}$.

Vậy khẳng định b) sai.

+ Do O là giao điểm hai đường chéo AC và BD của hình bình hành ABCD nên O là trung điểm của AC và BD.

Khi đó ta có: $\overrightarrow {OA} = \overrightarrow {CO} ;\;\overrightarrow {OD} = \overrightarrow {BO}$

Do đó: $\left\{ {\begin{array}{*{20}{l}}{\overrightarrow {OA} + \overrightarrow {OB} = \overrightarrow {CO} + \overrightarrow {OB} = \overrightarrow {\overrightarrow {CB} = - \overrightarrow {BC} } }\\{\overrightarrow {OC} + \overrightarrow {OD} = \overrightarrow {OC} + \overrightarrow {BO} = \overrightarrow {\overrightarrow {BO} + \overrightarrow {OC} = \overrightarrow {BC} } }\end{array}} \right.$

Suy ra: $\overrightarrow {OA} + \overrightarrow {OB} = - \left( {\overrightarrow {OC} + \overrightarrow {OD} } \right)$.

Vậy khẳng định c) sai.