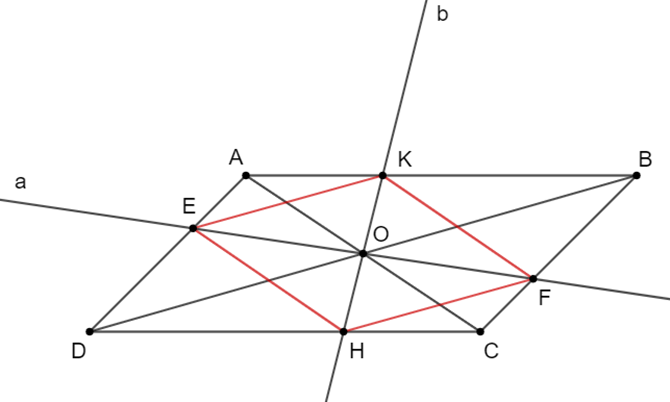
Cho hình bình hành ABCD. Gọi O là giao điểm 2 đường chéo AC và BD. Qua O vẽ đường thẳng a cắt AD, BC lần lượt tại E, F.
Cho hình bình hành ABCD. Gọi O là giao điểm 2 đường chéo AC và BD. Qua O vẽ đường thẳng a cắt AD, BC lần lượt tại E, F. Qua O vẽ đường thẳng b cắt AB và CD lần lượt tại K, H. Chứng minh tứ giác EKFH là hình bình hành.