Cho hình bình hành ABCD, đường chéo BD. Kẻ AH và CK vuông góc với BD ở H
Cho hình bình hành ABCD, đường chéo BD. Kẻ AH và CK vuông góc với BD ở H và ở K. Chứng minh tứ giác AHCK là hình bình hành.
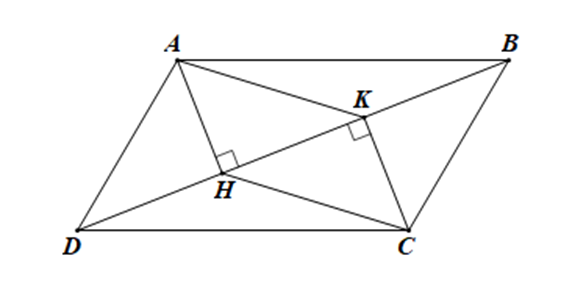
Ta có:
AH ⊥ BD, CK ⊥ BD ⇒ AH // CK (1)
∆ABH và ∆CDK có:
\(\widehat {AHB} = \widehat {CKD}\) (= 90°)
\(\widehat {ABH} = \widehat {CDK}\) (2 góc so le trong)
AB = CD (tính chất hình bình hành)
⇒ ∆ABH = ∆CDK (cạnh huyền – góc nhọn)
⇒ AH = CK (2)
Từ (1), (2) ⇒ tứ giác AHCK là hình bình hành. \[\]