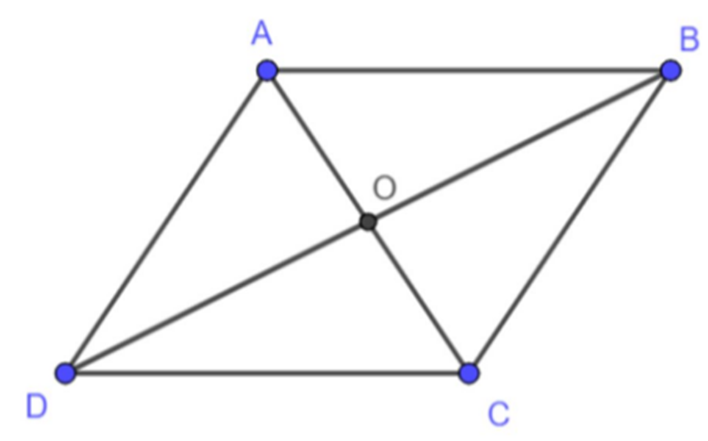
Cho hình bình hành ABCD có tâm O. M là một điểm bất kì trong mặt phảng.CMR
50
04/05/2024
Cho hình bình hành ABCD có tâm O. M là một điểm bất kì trong mặt phảng.CMR:
a) \[\overrightarrow {{\rm{AB}}} {\rm{ + }}\overrightarrow {{\rm{ OD}}} {\rm{ + }}\overrightarrow {{\rm{OC}}} = \overrightarrow {AC} \]
b) \[\overrightarrow {{\rm{BA}}} {\rm{ + }}\overrightarrow {{\rm{BC}}} {\rm{ + }}\overrightarrow {{\rm{OB}}} = \overrightarrow {OD} \]
c) \[\overrightarrow {{\rm{BA}}} {\rm{ + }}\overrightarrow {{\rm{BC}}} {\rm{ + }}\overrightarrow {{\rm{ OB}}} = \overrightarrow {MO} - \overrightarrow {MB} \]
Trả lời
a) \[\overrightarrow {{\rm{AB}}} {\rm{ + }}\overrightarrow {{\rm{ OD}}} {\rm{ + }}\overrightarrow {{\rm{OC}}} \]
\[{\rm{ = }}\overrightarrow {{\rm{AB}}} {\rm{ + (}}\overrightarrow {{\rm{OC}}} {\rm{ - }}\overrightarrow {{\rm{OB}}} {\rm{)}}\](quy tắc trừ hai vec tơ)
\[{\rm{ = }}\overrightarrow {{\rm{AB}}} {\rm{ + }}\overrightarrow {{\rm{BC}}} {\rm{ = }}\overrightarrow {{\rm{AC}}} \]
b) \[\overrightarrow {{\rm{BA}}} {\rm{ + }}\overrightarrow {{\rm{BC}}} {\rm{ + }}\overrightarrow {{\rm{OB}}} \] (quy tắc hình bình hành)
\[{\rm{ = }}\overrightarrow {{\rm{BD}}} {\rm{ + }}\overrightarrow {{\rm{OB}}} {\rm{ = }}\overrightarrow {{\rm{OD}}} \]
c) \[\overrightarrow {{\rm{BA}}} {\rm{ + }}\overrightarrow {{\rm{BC}}} {\rm{ + }}\overrightarrow {{\rm{ OB}}} \]
\[{\rm{ = }}\overrightarrow {{\rm{BD}}} {\rm{ + }}\overrightarrow {{\rm{OB}}} {\rm{ = }}\overrightarrow {{\rm{OD}}} {\rm{ = }}\overrightarrow {{\rm{BO}}} {\rm{ = }}\overrightarrow {{\rm{MO}}} {\rm{ - }}\overrightarrow {{\rm{MB}}} \]