Cho hình bình hành ABCD, có góc A = 60 độ. Lấy các điểm E, F theo thứ tự thuộc
Cho hình bình hành ABCD, có ˆA=60∘. Lấy các điểm E, F theo thứ tự thuộc cạnh AD, CD sao cho DE = CF. Gọi K là điểm đối xứng với F qua BC. Chứng minh EK // AB.
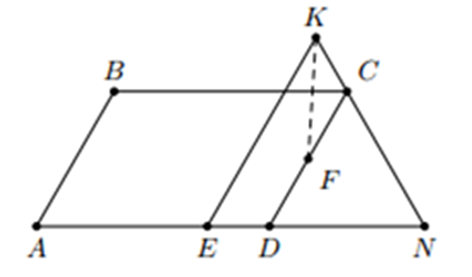
Kéo dài KC cắt AD tại N
Ta có AB // CD nên ^BAD=^CDN=60∘
K đối xứng với F qua BC nên ^BCD=^KCB=60∘
^CND=^KCB=60∘
⇒ Tam giác CND đều ⇒ CN = DN
Lại có CK = DE (cùng = CF)
KN = EN ⇒ tam giác KNE đều
⇒ ^KEN=^CDN=60∘
⇒ KE // CD // AB