Cho hình bình hành ABCD có BC = 2AB và góc A = 60^0. Gọi E, F theo thứ tự là trung điểm của BC và AD. a) Tứ giác ECDF là hình gì? Vì sao? b) Tam giác DEC là tam giác gì? Vì sao? c) Tính số
34
12/05/2024
Cho hình bình hành ABCD có BC = 2AB và \[\widehat A = 60^\circ \]. Gọi E, F theo thứ tự là trung điểm của BC và AD.
a) Tứ giác ECDF là hình gì? Vì sao?
b) Tam giác DEC là tam giác gì? Vì sao?
c) Tính số đo\[\widehat {AED}\]?
Trả lời
Lời giải
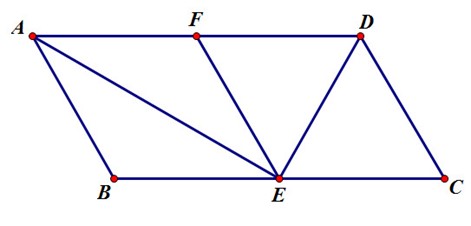
a) Ta có \[\left\{ \begin{array}{l}BC = 2AD = 2AB = 2AE = 2FD\\BC = 2BE = 2EC\end{array} \right.\]
Suy ra AB = BE = EC = CD = FD = AF
Tứ giác ECFD có \[\left\{ \begin{array}{l}FD//EC\\FD = EC\end{array} \right.\]
Do đó tứ giác ECFD là hình bình hành.
b) ∆ DEC có: \[\left\{ \begin{array}{l}DC = EC\\\widehat A = \widehat C = 60^\circ \end{array} \right.\] ⇒ ∆ DEC là ∆ đều
c) Ta có: tứ giác ABEF là hình bình hành nên AB // FE ⇒ \[\widehat {AEF} = \widehat {EAB}\] (1)
• Xét ∆AFE có AF = FE nên ∆AFE là tam giác cân.
Do đó \[\widehat {FAE} = \widehat {FEA}\] (2)
Từ (1) và (2) suy ra \[\widehat {BAE} = \widehat {EAF} = \widehat {FEA} = \frac{{60^\circ }}{2} = 30^\circ \].
• Xét ∆FED có \[\left\{ \begin{array}{l}FD = DC = DE\\\widehat {FDE} = 60^\circ \end{array} \right.\] nên ∆FED là tam giác đều.
Suy ra \[\widehat {FDE} = \widehat {DEF} = \widehat {EFD} = \frac{{180^\circ }}{3} = 60^\circ \].
Ta có \[\widehat {AED} = \widehat {AEF} + \widehat {FED} = 30^\circ + 60^\circ = 90^\circ \]

