Cho hình bình hành ABCD có AB > BC. Đướng phân giác của góc D cắt AB tại M, đường phân giác của góc B cắt CD tại N a) Chứng minh AM = CN b) Chứng minh tứ giác BMDN là hình bình hành. c) Gọi H
Lời giải
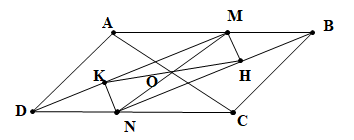
a) Vì ABCD là hình bình hành nên AB // CD
Suy ra ^AMD=^MDC (Hai góc so le trong) và AB = CD, AD = BC (1)
Vì DM là tia phân giác của góc ADC ⇒ ^ADM=^MDC=12^CDA
Suy ra ^AMD=^MDA
Do đó tam giác ADM cân tại A
Suy ra AM = AD (tính chất) (2)
Vì BN là tia phân giác của góc ABC ⇒ ^ABN=^NBC=12^ABC
Vì ABCD là hình bình hành nên AB // CD nên ^ABN=^BNC (Hai góc so le trong)
Suy ra ^CBN=^BNC
Do đó tam giác BCN cân tại C
Suy ra CN = CB (tính chất) (3)
Từ (1), (2) và (3) suy ra AM = CN
Vậy AM = CN
b) Ta có:
AB = AM + MB
CD = CN + ND
Mà AB = CD, AM = CN (chứng minh câu a)
Suy ra MB = ND
Tứ giác DMBN có:
MB = ND (chứng minh trên)
MB // ND (vì AB // CD)
Suy ra DMBN là hình bình hành
Vậy DMBN là hình bình hành.
c) Vì DMBN là hình bình hành nên DM // BN, DM = BN
Ta có DM // BN, NK ⊥ DM
Nên NK ⊥ BN (quan hệ từ vuông góc đến song song)
Suy ra ^KNH=90∘
Vì DM // BN, MH ⊥ BN
Nên DM ⊥ MH (quan hệ từ vuông góc đến song song)
Suy ra ^HMK=90∘
Vì H,K lần lượt là hình chiếu M và N trên BN và DM
Nên ^MKN=90∘,^MHN=90∘
Xét tứ giác MHNK có
^MKN=90∘,^MHN=90∘, ^KNH=90∘, ^HMK=90∘ (chứng minh trên)
Suy ra MHNK là hình chữ nhật
Vậy MHNK là hình chữ nhật.
d)Vì ABCD là hình bình hành nên AC và BD cắt nhau tại trung điểm của mỗi đường
Gọi O là trung điểm của AC (*)
Suy ra O là trung điểm của BD
Vì DMBN là hình bình hành nên MN và BD cắt nhau tại trung điểm của mỗi đường
Mà O là trung điểm của BD
Suy ra O là trung điểm của MN (**)
Vì MHNK là hình chữ nhật nên MN và HK cắt nhau tại trung điểm của mỗi đường
Mà O là trung điểm của MN
Suy ra O là trung điểm của HK (***)
Từ (*), (**) và (***) suy ra ba đường thẳng AC, MN, KH đồng quy tại điểm O
Vậy ba đường thẳng AC, MN, KH đồng quy.