Cho hình bình hành ABCD có AB = 2BC. Gọi E và F theo thứ tự là trung điểm của AB, CD.

a) Chứng minh DEBF là hình bình hành.

b) Chứng minh ADFE là hình thoi.

c) Gọi M là giao điểm của DE và AF, N là giao điểm của CE và BF. Chứng minh EMFN là hình chữ nhật.

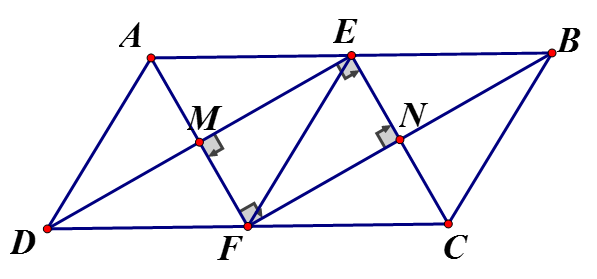
a) Ta có: AB = DC (tính chất hình bình hành) mà E, F lần lượt là trung điểm AB, CD

⇒ EB = DF và EB // DF

⇒ BEDF là hình bình hành

b) AE = DF(= $\frac{1}{2}$  AB = $\frac{1}{2}$  DC) và AE // DF

⇒ AEFD là hình bình hành

Mà AE = AD (= $\frac{1}{2}$  AB)

⇒ AEFD là hình thoi

c) EBFD là hình bình hành ⇒ ED // BF ⇒ EM // FN(1)

Chứng minh tương tự câu b ⇒ EBCF là hình thoi

Và AEFD, EBCF là hình thoi

⇒ EM = FN và FN = NB mà ED = BF ⇒ ME = FN(2)

Từ (1) và (2) suy ra EMFN là hình bình hành mà   $\widehat{EMF}$ = 90°(AEFD là hình thoi)

⇒ EMFN là hình chữ nhật.