Lời giải
Đáp án đúng là: D
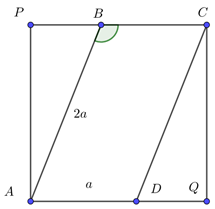
Dựng hình chữ nhật APCQ.
Khi hình bình hành ABCD quay quanh cạnh AD, ta quay hình chữ nhật APCQ quanh cạnh AQ, sau đó bỏ đi hai khối nón bằng nhau ở hai đầu (được tạo thành khi quay tam giác ABP và tam giác CDQ quanh cạnh AD).
Ta có ABCD là hình bình hành. Suy ra \(\widehat {ADC} = \widehat {ABC} = 120^\circ \).
Ta có: \(\widehat {CDQ} + \widehat {ADC} = 180^\circ \) (hai góc kề bù).
\( \Leftrightarrow \widehat {CDQ} = 180^\circ - \widehat {ADC} = 180^\circ - 120^\circ = 60^\circ \).
Tam giác CDQ vuông tại Q: \(\sin \widehat {CDQ} = \frac{{CQ}}{{CD}}\).
⇒ CQ = 2a.sin60° = \(a\sqrt 3 \).
Tam giác CDQ vuông tại Q: \(\cos \widehat {CDQ} = \frac{{DQ}}{{DC}}\).
⇒ DQ = 2a.cos60° = a.
Ta có AQ = AD + DQ = AD + PB = a + a = 2a.
Thể tích khối tròn xoay cần tìm là: \(V = {V_{APCQ}} - 2{V_{CDQ}} = \pi .C{Q^2}.AQ - 2.\frac{1}{3}\pi .C{Q^2}.DQ\)
\( = \pi .3{a^2}.2a - 2.\frac{1}{3}\pi .3{a^2}.a = 4\pi {a^3}\).
Vậy ta chọn phương án D.