Cho hình bình hành ABCD (AB > BC). Tia phân giác của góc D cắt AB ở E, tia phân giác của góc B cắt CD ở F.

a) Chứng minh rằng DE // BF.

b) Tứ giác DEBF là hình gì? Vì sao?

Lời giải

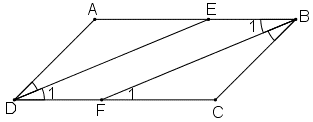
a) Ta có:

ABCD là hình bình hành ⇒ AB // CD ⇒ $\widehat {{B_1}} = \widehat {{F_1}}$ (Hai góc so le trong) (1)

Vì DE là tia phân giác của góc D ⇒ $\widehat {{D_1}} = \frac{1}{2}\widehat D$

Vì BF là tia phân giác của góc B ⇒ $\widehat {{B_1}} = \frac{1}{2}\widehat B$

Mà $\widehat B = \widehat D$ ( Do ABCD là hình bình hành)

⇒ $\widehat {{B_1}} = \widehat {{D_1}}$                                                    (2)

Từ (1) và (2) suy ra $\widehat {{D_1}} = \widehat {{F_1}}\left( { = \widehat {{B_1}}} \right)$

Mà hai góc này ở vị trí đồng vị ⇒ DE // BF (đpcm)

Vậy DE // BF

b) Tứ giác DEBF có:

DE // BF (chứng minh ở câu a)

BE // DF (vì AB // CD)

⇒ DEBF là hình bình hành

Vậy DEBF là hình bình hành.