Cho hình bình hành ABCD (AB > AD). Qua A kẻ đường thẳng vuông góc với BD tại E, cắt CD tại I. Qua C kẻ đường thẳng vuông góc với AB tại F, cắt AB tại K. a) Tứ giác AKCI là hình gì? Vì sao? b
39
18/05/2024
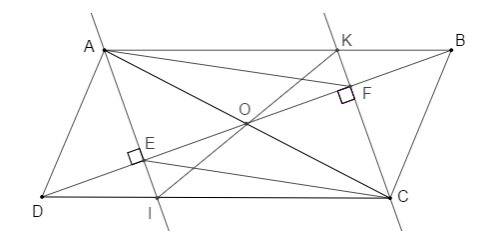
Cho hình bình hành ABCD (AB > AD). Qua A kẻ đường thẳng vuông góc với BD tại E, cắt CD tại I. Qua C kẻ đường thẳng vuông góc với AB tại F, cắt AB tại K.
a) Tứ giác AKCI là hình gì? Vì sao?
b) Chứng minh AF // CE
c) Chứng minh rằng ba đường thẳng AC, EF và KI đồng quy tại một điểm.
Trả lời
Lời giải
a) Vì ABCD là hình bình hành nên AB // DC
Hay AK // IC
Ta có AI ⊥ BD và CK ⊥ BD
Suy ra AI // CK
Xét tứ giác AKCI có AI // CK, AK // CI
Suy ra AKCI là hình bình hành
Vậy AKCI là hình bình hành.
b) Vì ABCD là hình bình hành nên AB = CD
Vì AB // CD nên ^ABE=^CDF (hai góc so le trong)
Xét ΔABE và ΔCDF có:
^AEB=^CFD(=90∘)
AB = CD (chứng minh trên)
^ABE=^CDF (chứng minh trên)
Suy ra ΔABE = ΔCDF (cạnh huyền – góc nhọn)
Do đó AF = CF (hai cạnh tương ứng)
Xét tứ giác AECF có AE // CF, AF = CF
Nên AECF là hình bình hành
Suy ra AF // CE
Vậy AF // CE.
c) Gọi giao điểm của AC và KI là O
Vì AKCI là hình bình hành nên O là trung điểm của AC, KI
Vì AECF là hình bình hành, O là trung điểm của AC
Nên O là trung điểm của EF
Suy ra AC, EF và KI đồng quy tại O
Vậy ba đường thẳng AC, EF và KI đồng quy tại một điểm.

