Cho hàm số y = x + 1 có đồ thị là (d) và hàm số y = -x + 3 có đồ thị là (d'): a, Vẽ (d)
44
11/06/2024
Cho hàm số y = x + 1 có đồ thị là (d) và hàm số y = –x + 3 có đồ thị là (d'):
a, Vẽ (d) và (d') trên cùng 1 mặt phẳng tọa độ.
b, Hai đường thẳng (d) và (d') cắt nhau tại C và cắt trục Ox theo thứ tự A và B. Tìm tọa độ các điểm A, B, C (tìm tọa độ điểm C bằng phương pháp đại số).
c, Tính chu vi và diện tích của tam giác ABC (với đơn vị đo trên các trục tọa độ là cm).
d, Tính góc tạo bởi đường thẳng y = x + 1 với trục Ox.
Trả lời
a)
Đường thẳng (d) đi qua hai điểm (0; 1) và (–1; 0).
Đường thẳng (d’) đi qua hai điểm (0; 3) và (3; 0).
Hình vẽ:
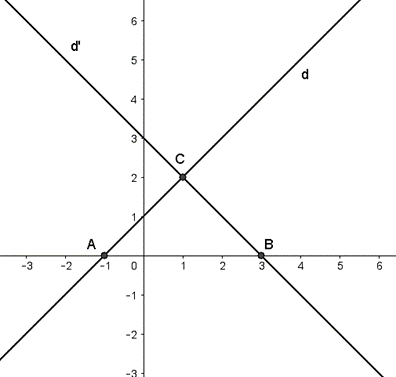
b)
Tọa độ điểm A(–1; 0) và B(3; 0) như hình vẽ.
Gọi điểm C(x0; y0)
Tọa độ của điểm C là nghiệm của hệ phương trình:
{y0=x0+1y0=−x0+3⇔{x0−y0=−1−x0−y0=−3⇔{x0=1y0=2
Do đó, C(1; 2)
c)
Ta có:
→AB=(4;0)⇒|→AB|=AB=4 (cm)
→AC=(2;2)⇒|→AC|=AC=2√2 (cm)
→BC=(−2;2)⇒|→BC|=BC=2√2 (cm)
Chu vi tam giác ABC là: C = AB + AC + BC = 4+4√2 (cm)
d)
Góc tạo bởi y = x + 1 với Ox chính là góc ^CAB
Xét tam giác ABC
Ta có:
CB2=CA2+AB2−2CA.AB.cos^CAB⇒cos^CAB=CA2+AB2−CB22CA.AB=(2√2)2+42−(2√2)22.2√2.4=√22⇒^CAB=45∘

