Lời giải
a) Với M(–1; –1) ∈ (1), ta có –1 = –m + 1.
Suy ra m = 2.
Khi đó y = 2x + 1.
Bảng giá trị:
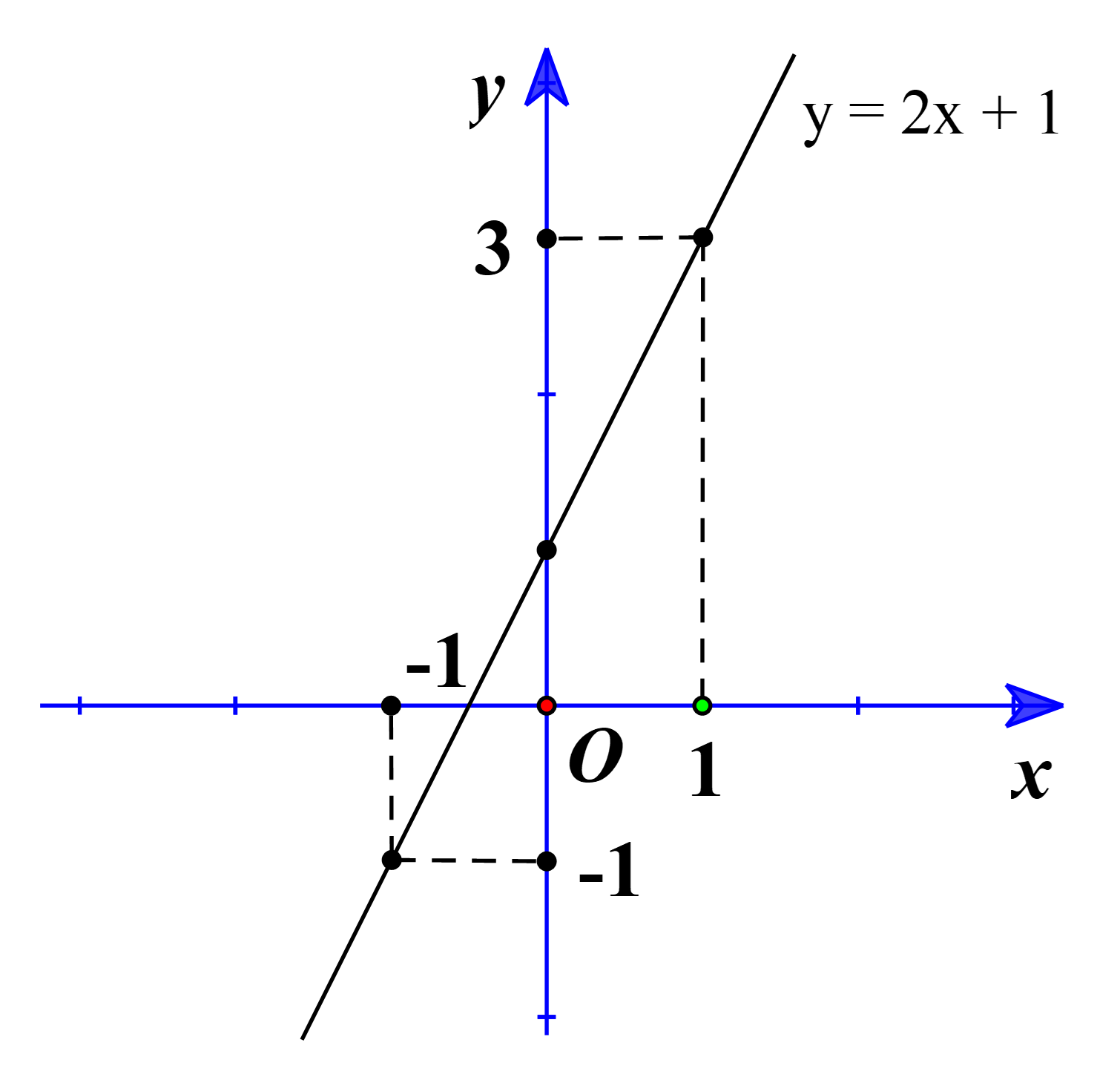
b) Theo đề, ta có (1) // (d).
Suy ra \(\left\{ \begin{array}{l}m = {m^2} - 2\\1 \ne 2m + 3\end{array} \right.\)
Khi đó \(\left\{ \begin{array}{l}{m^2} - m - 2 = 0\\2m \ne - 2\end{array} \right.\)
Vì vậy \(\left\{ \begin{array}{l}\left[ \begin{array}{l}m = 2\\m = - 1\end{array} \right.\\m \ne - 1\end{array} \right.\)
Suy ra m = 2.
Vậy m = 2 thỏa mãn yêu cầu bài toán.
c) Thế x = 0 vào phương trình (1), ta được y = 1.
Suy ra đồ thị (1) luôn đi qua điểm A(0; 1).
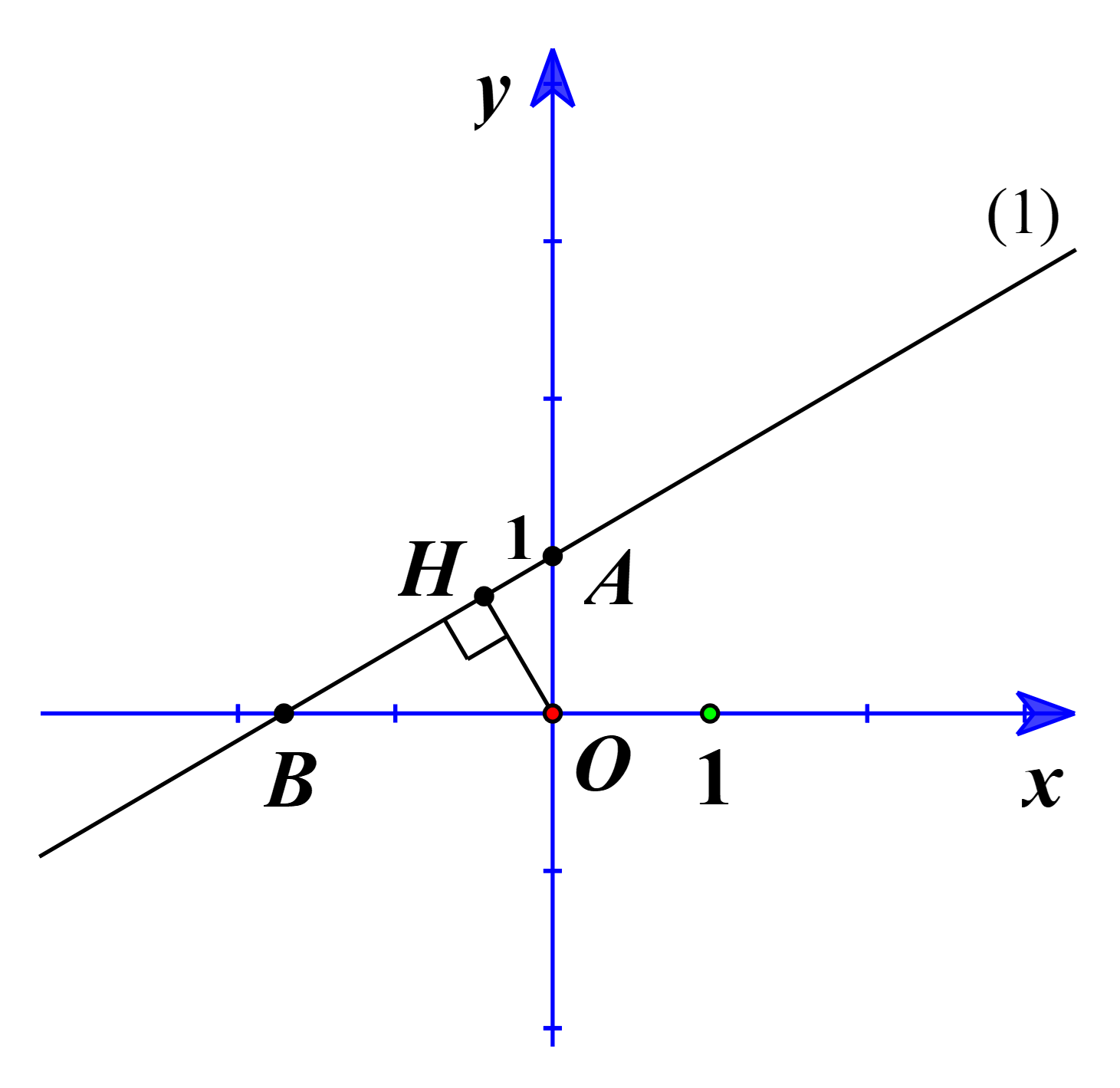
Phương trình hoành độ giao điểm của (1) và trục Ox: mx + 1 = 0.
\( \Leftrightarrow x = - \frac{1}{m}\,\,\,\left( {m \ne 0} \right)\).
Suy ra giao điểm của (1) và trục Ox là điểm \(B\left( { - \frac{1}{m};0} \right)\).
Ta có \(OA = 1,\,OB = \left| { - \frac{1}{m}} \right|\).
Kẻ OH ⊥ AB tại H.
Tam giác ABO vuông tại O có OH là đường cao:
\(\frac{1}{{O{H^2}}} = \frac{1}{{O{A^2}}} + \frac{1}{{O{B^2}}}\) (hệ thức lượng trong tam giác vuông).
\( \Leftrightarrow \frac{1}{{O{H^2}}} = 1 + {m^2}\)
\( \Leftrightarrow O{H^2} = \frac{1}{{{m^2} + 1}}\)
Suy ra \(OH = \frac{1}{{\sqrt {{m^2} + 1} }}\).
Theo đề, ta có khoảng cách từ gốc tọa độ O đến đồ thị hàm số (1) bằng \(\frac{2}{{\sqrt 5 }}\).
Suy ra \(OH = \frac{2}{{\sqrt 5 }}\).
\( \Leftrightarrow \frac{1}{{\sqrt {{m^2} + 1} }} = \frac{2}{{\sqrt 5 }}\)
\( \Leftrightarrow \sqrt {{m^2} + 1} = \frac{{\sqrt 5 }}{2}\)
\( \Leftrightarrow {m^2} + 1 = \frac{5}{4}\)
\( \Leftrightarrow {m^2} = \frac{1}{4}\)
\( \Leftrightarrow m = \pm \frac{1}{2}\) (nhận).
Vậy \(m = \pm \frac{1}{2}\) thỏa mãn yêu cầu bài toán.


