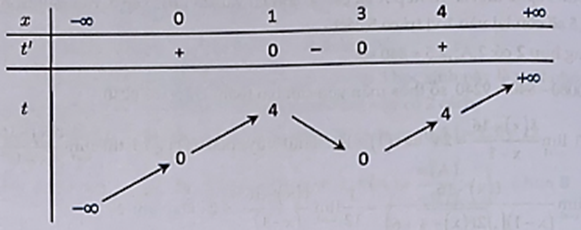
Cho hàm số y = f(x) liên tục trên R và có đồ thị như hình bên. Với tham số thực m thuộc 0 4 thì phương trình f x x-3 ^2 = m có ít nhất bao nhiêu nghiệm thực thuộc [0;4)?
Cho hàm số y = f(x) liên tục trên R và có đồ thị như hình bên. Với tham số thực thì phương trình có ít nhất bao nhiêu nghiệm thực thuộc [0;4)?