Cho hàm số y = f(x) có đồ thị như hình vẽ. Đặt g(x) = f(f(x) - 1). Tìm số nghiệm của phương trình g'(x) = 0.
Cho hàm số y = f(x) có đồ thị như hình vẽ.
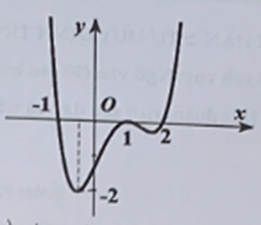
Đặt g(x) = f(f(x) - 1). Tìm số nghiệm của phương trình g'(x) = 0.
Cho hàm số y = f(x) có đồ thị như hình vẽ.

Đặt g(x) = f(f(x) - 1). Tìm số nghiệm của phương trình g'(x) = 0.
Ta có
+) Với
+) Với
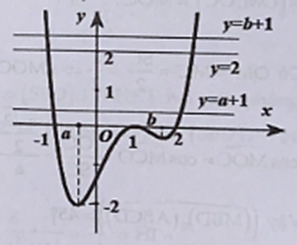
Từ đồ thị hàm số f(x) ta có:
- Phương trình (1) có 2 nghiệm.
- Phương trình (2) có 2 nghiệm không trùng với 2 nghiệm của phương trình (1).
- Phương trình (3) có 2 nghiệm không trùng với 2 nghiệm của phương trình (1) và 2 nghiệm của phương trình (2).
Vậy phương trình g'(x) = 0 có tất cả 9 nghiệm.