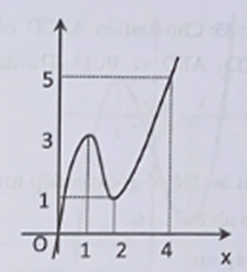
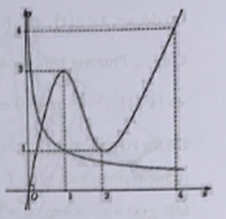
Cho hàm số y = f(x) có đạo hàm liên tục trên R và f(0) = 0; f(4) > 4. Biết hàm y = f'(x) có đồ thị như hình vẽ bên. Số điểm cực trị của hàm số $g\left(x\right)=\left|f\left(x^2\right)-2x\right|$ là

Chọn D

Xét $h\left(x\right)=f\left(x^2\right)-2x$

$\Rightarrow h^{\text{'}}\left(x\right)=2x{f}^{\text{'}}\left(x^2\right)-2=2\left[x{f}^{\text{'}}\left(x^2\right)-1\right],h^{\text{'}}\left(x\right)=0\iff x{f}^{\text{'}}\left(x^2\right)-1=0.$

Nếu $x\le 0$ thì phương trình vô nghiệm vì $f^{\text{'}}\left(x^2\right)\ge 0,\forall x$ nên

Nếu x > 0, đặt $x^2=t\Rightarrow f^{\text{'}}\left(t\right)=\frac{1}{\sqrt{t}}$ có nghiệm duy nhất $t=a\in (0;1)$

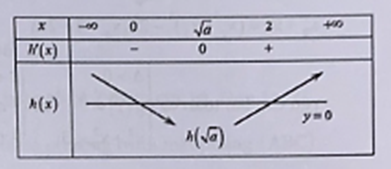
Vì $\left\{\begin{array}{l}h\left(0\right)=0\\ h\left(2\right)>0\end{array}\right.$nên ta có bảng biến thiên của h(x0) như sau: