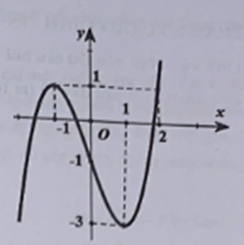
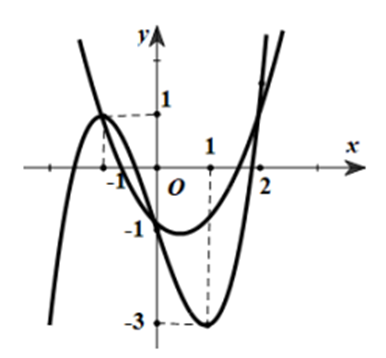
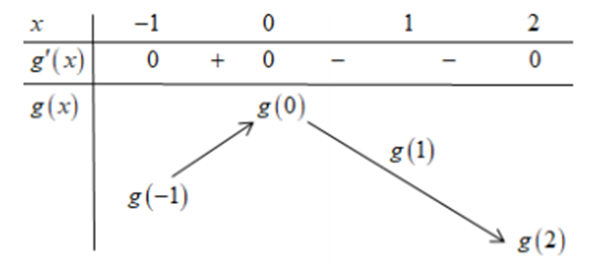
Cho hàm số y = f(x) có đạo hàm liên tục trên R và có đồ thị y = f'(x) như hình vẽ bên. Gọi g(x) = f(x) -1/3x^3 + 1/2x^2 + x - 2021 .Biết g(-1) + g(1) > g(0) + g(2).
Cho hàm số y = f(x) có đạo hàm liên tục trên R và có đồ thị y = f'(x) như hình vẽ bên. Gọi .Biết g(-1) + g(1) > g(0) + g(2). Với thì g(x) có giá trị nhỏ nhất tại g(xo). Tìm xo.