Cho hàm số y = f(x) có bảng biến thiên như sau:
Cho hàm số y = f(x) có bảng biến thiên như sau:
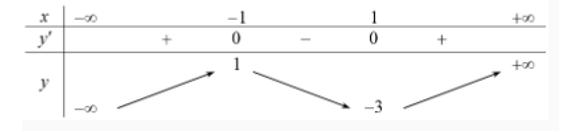
Có bao nhiêu giá trị nguyên của tham số để hàm số có đúng 5 điểm cực trị?
Cho hàm số y = f(x) có bảng biến thiên như sau:

Có bao nhiêu giá trị nguyên của tham số để hàm số có đúng 5 điểm cực trị?
Ta có số điểm cực trị của hàm số và hàm số bằng nhau.
Hàm số là hàm số chẵn nên có đồ thị nhận Oy làm trục đối xứng.
Do đó, để hàm số có 5 điểm cực trị thì hàm số có hai điểm cực trị lớn hơn 0.
Ta có: .
Do nên để hàm sổ có hai điểm cực trị lớn hơn 0 thì .
Do m nguyên thuộc đoạn [-20; 20] nên .
Vậy có 19 giá trị m nguyên thỏa mãn yêu cầu bài toán.