Cho hàm số y = f(x) có đồ thị như hùnh vẽ bên. Có bao nhiêu giá trị nguyên của tham số m để hàm số g(x) = f x + 2020 + m 2 có 5 điểm cực trị?
Cho hàm số y = f(x) có đồ thị như hùnh vẽ bên. Có bao nhiêu giá trị nguyên của tham số m để hàm số có 5 điểm cực trị?
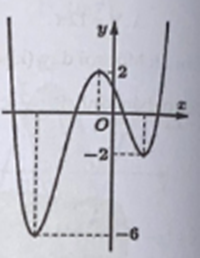
A. 1
B. 2
C. 4
D. 5
