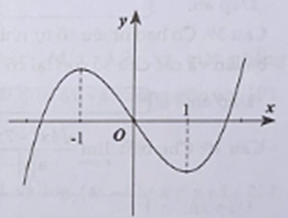
Cho hàm số y = f(x) có đạo hàm trên R và f(1) = 1. Đồ thị hàm số y = f'(x) như hình bên. Có bao nhiêu số nguyên dương a để hàm số nghịch biến trên
Cho hàm số y = f(x) có đạo hàm trên R và f(1) = 1. Đồ thị hàm số y = f'(x) như hình bên. Có bao nhiêu số nguyên dương a để hàm số y=|4f(sinx)+cos2x−a| nghịch biến trên (0;π2)?
A. 2
B. 3
C. Vô số
D. 5
