Cho hàm số y = f (x). Hàm số y = f ¢(x) có bảng biến thiên như sau: Bất phương trình f (x) < ex + m đúng với mọi x Î (−1; 1) khi và chỉ khi:
36
13/08/2024
Cho hàm số y = f (x). Hàm số y = f ¢(x) có bảng biến thiên như sau:
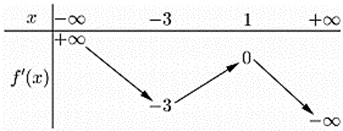
Bất phương trình f (x) < ex + m đúng với mọi x Î (−1; 1) khi và chỉ khi:
Trả lời
Lời giải
Theo đề bài ta có:
f (x) < ex + m Û f (x) − ex < m
Đặt g (x) = f (x) − ex.
Khi đó: f (x) < ex + m với mọi x Î (−1; 1)
Þ g (x) = f (x) − ex < m với mọi x Î (−1; 1)
⇔m≥max
g¢ (x) = f¢ (x) − ex
Trên (−1; 1) ta có:
f ¢ (x) < 0; ex > 0 "x Î ℝ
Þ g¢ (x) < 0 "x Î (−1; 1)
Þ g (x) nghịch biến trên (−1; 1)
\Rightarrow \mathop {\max \;}\limits_{\left[ { - 1;\;1} \right]} g\left( x \right) = g\left( { - 1} \right) = f\left( { - 1} \right) - {e^{ - 1}} = f\left( { - 1} \right) - \frac{1}{e}
\Rightarrow m \ge f\left( { - 1} \right) - \frac{1}{e}
Vậy bất phương trình f (x) < ex + m đúng với mọi x Î (−1; 1) khi và chỉ khi:
m \ge f\left( { - 1} \right) - \frac{1}{e}.

