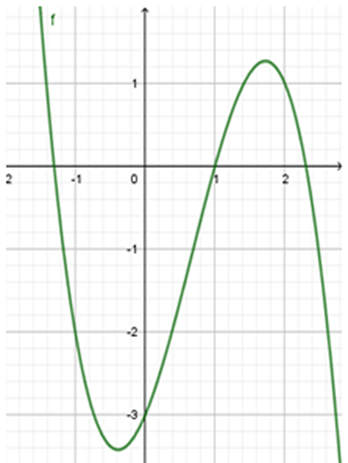
Cho hàm số y = ax^3 + bx^2 + cx + d có đồ thị như hình vẽ. Tìm mệnh đề đúng
32
02/09/2024
Cho hàm số y = ax3 + bx2 + cx + d có đồ thị như hình vẽ. Tìm mệnh đề đúng.
A. a < 0, b > 0, c > 0, d < 0.
B. a < 0, b < 0, c > 0, d < 0.
C. a > 0, b > 0, c > 0, d < 0.
D. a < 0, b > 0, c < 0, d < 0.
Trả lời
Đáp án đúng là: A.
Ta thấy lim ⇒ a < 0.
Đồ thị hàm số cắt trục Oy tại điểm có tung độ y0 = −3 ⇒ d < 0.
Đồ thị hàm số có 2 điểm cực trị trái dấu nên y' = 3a{x^2} + 2bx + c = 0 có 2 nghiệm trái dấu
⇒ 3ac < 0 ⇒ c > 0
Hoành độ điểm uốn nằm bên phải trục tung nên y'' = 6ax + 2b = 0 có nghiệm dương
⇒ x = \frac{{ - b}}{{3a}} > 0 ⇔ \frac{b}{a} < 0 ⇒ b > 0
Vậy a < 0, b > 0, c > 0, d < 0.