Cho hàm số y = (2m − 1)x + 2 − m có đồ thị là đường thẳng (d).

a) Tìm m để hàm số đồng biến? Hàm số nghịch biến?

b) Tìm m để (d) cắt Ox tại điểm có hoành độ bằng 3.

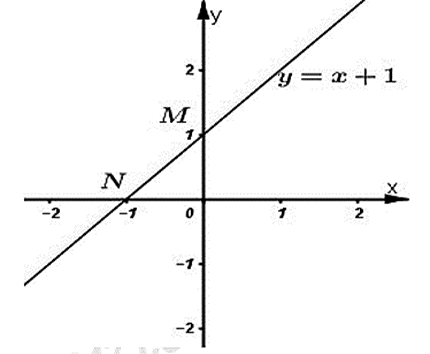
c) Tìm m để (d) song song với đường thẳng y = x + 3. Với giá trị của m vừa tìm được hãy vẽ đường thẳng (d); gọi giao điểm của (d) với Ox và Oy lần lượt là M, N. Tính diện tích tam giác OMN.

d) Cho các đường thẳng d₁: 2x − y + 7 = 0; d₂: x + y − 1 = 0. Tìm m để 3 đường thẳng d; d₁; d₂ đồng quy.

a) Hàm số đồng biến khi $2m - 1 > 0 \Leftrightarrow m > \frac{1}{2}$

Hàm số nghịch biến khi $2m - 1 < 0 \Leftrightarrow m < \frac{1}{2}$

b) d đi qua điểm (3; 0) Û 0 = 3(2m − 1) + 2 − m

$\Leftrightarrow m = \frac{1}{5}$

c) $d\;{\rm{//}}\;y = x + 3 \Leftrightarrow \left\{ \begin{array}{l}2m - 1 = 1\\2 - m \ne 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m = 1\\m \ne - 1\end{array} \right. \Leftrightarrow m = 1$

Þ d: y = x + 1.

Ta có đồ thị hàm số:

Ta có: OM = 1; ON = |−1| = 1

$\Rightarrow {S_{OMN}} = \frac{1}{2}OM\,.\,ON = \frac{1}{2}$

Vậy ${S_{OMN}} = \frac{1}{2}$.

d) Gọi I là giao điểm của d₁; d₂. Khi đó tọa độ điểm I là nghiệm của hệ phương trình: 

$\left\{ \begin{array}{l}2x - y + 7 = 0\\x + y - 1 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}2x - y = - 7\\x + y = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = - 2\\y = 3\end{array} \right.$

Suy ra I(−2; 3).

Mà I Î d Þ 3 = −2(2m − 1) + 2 − m

Û 3 = −4m + 2 + 2 − m

Û 5m = 1

$\Leftrightarrow m = \frac{1}{5}$.

Vậy $m = \frac{1}{5}$ là giá trị cần tìm.