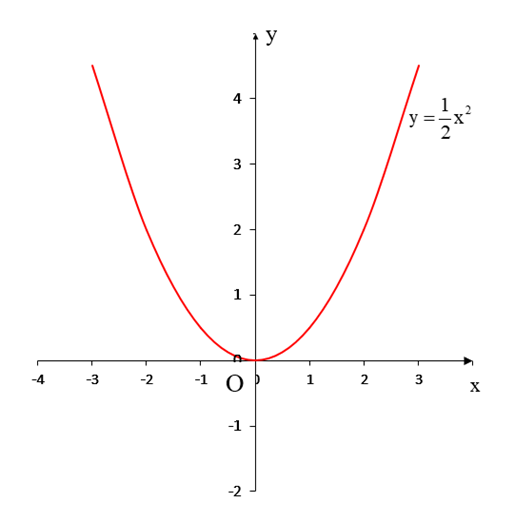
b) Điểm cách đều hai trục tọa độ nằm trên đường thẳng: y = x hoặc y = – x.
Xét phương trình hoành độ giao điểm của parabol (P)\(y = \frac{1}{2}{x^2}\) và đường thẳng y = x:
\(\frac{1}{2}{x^2} = x\)⟺ x2 – 2x = 0 ⇔ x(x – 2) = 0 \( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 0}\\{x = 2}\end{array}} \right.\)
• Với x = 0 ⇒ y = 0 ⇒ điểm O (0; 0)
• Với x = 2 ⇒ y = 2 ⇒ điểm A (2; 2)
Xét phương trình hoành độ giao điểm của parabol (P)\(y = \frac{1}{2}{x^2}\) và đường thẳng y = − x:
\(\frac{1}{2}{x^2} = - x\)⟺ x2 + 2x = 0 ⇔ x(x + 2) = 0 \( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 0}\\{x = - 2}\end{array}} \right.\)
Với x = 0 ⇒ y = 0 ⇒ điểm O (0; 0)
Với x = −2 ⇒ y = 2 ⇒ điểm B (−2; 2)
Vậy có hai đểm A (2; 2) và B (−2; 2) trên (P) cách đều hai trục tọa độ.
c) Gọi điểm\(M\left( {{x_0};\,\,\frac{9}{2}} \right)\)∈ (P)
\( \Rightarrow \frac{9}{2} = \frac{1}{2}{\left( {{x_0}} \right)^2} \Leftrightarrow {\left( {{x_0}} \right)^2} = 9\)\[ \Leftrightarrow {x_0} = \left| 3 \right| \Rightarrow {x_0} = \pm 3\] ;
Vậy \({M_1}\left( {3;\,\,\frac{9}{2}} \right)\); \({M_2}\left( { - 3;\,\,\frac{9}{2}} \right) \in \left( P \right)\) .