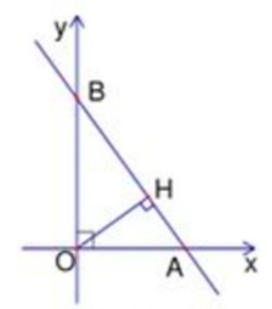
Đồ thị hàm số cắt trục hoành tại A, cắt trục tung tại B (A và B không trùng với gốc tọa độ O) nên đồ thị hàm số đã cho không đi qua gốc tọa độ và không song song với hai trục

Suy ra m – 2 ≠ 0 và m + 1 ≠ 0

Hay m ≠ 2 và m ≠ – 1

Khi đó \[{\rm{A}}\left( {\frac{{m + 1}}{{m - 2}};0} \right)\] và B(0; m + 1)

Suy ra \(OA = \left| {\frac{{m + 1}}{{m - 2}}} \right|\) và \(OB = \left| {m + 1} \right|\)

Xét tam giác AOB vuông tại O có OH ⊥ AB

Suy ra \(\frac{1}{{O{H^2}}} = \frac{1}{{O{A^2}}} + \frac{1}{{O{B^2}}}\) (hệ thức lượng trong tam giác vuông)

Hay \(\frac{1}{{O{H^2}}} = \frac{{{{\left( {m - 2} \right)}^2}}}{{{{\left( {m + 1} \right)}^2}}} + \frac{1}{{{{\left( {m + 1} \right)}^2}}}\)

⇔ \(\frac{1}{{{{\left( {\sqrt 2 } \right)}^2}}} = \frac{{{m^2} - 4m + 5}}{{{{\left( {m + 1} \right)}^2}}}\)

⇔ (m + 1)² = 2(m² – 4m + 5)

⇔ m² + 2m + 1 = 2m² – 8m + 10

⇔ m² – 10m + 9 = 0

⇔ (m – 1)(m – 9) = 0

⇔ \(\left[ \begin{array}{l}m = 1\\m = 9\end{array} \right.\)

Vậy m = 1 hoặc m = 9.