Lời giải
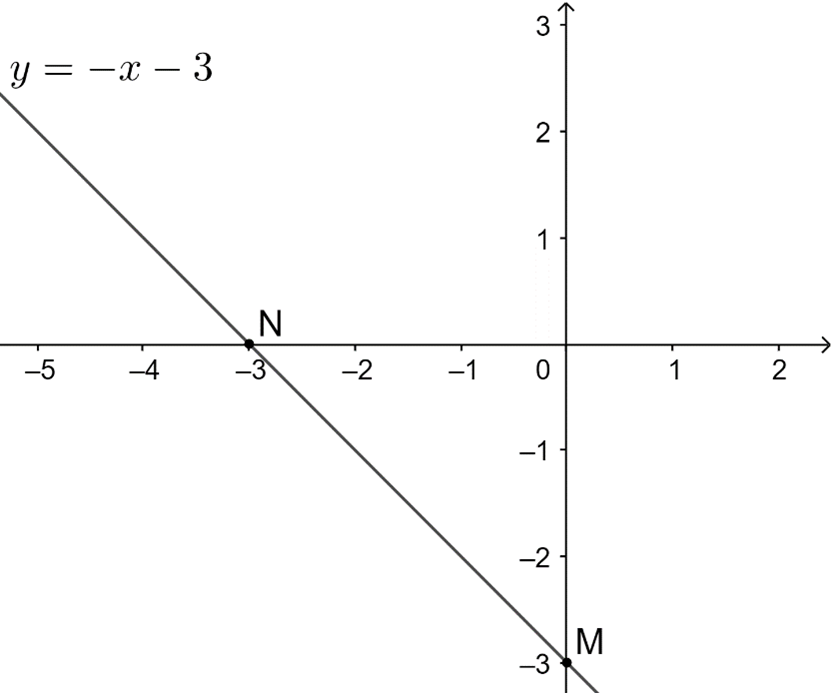
a) Với m = 0 Þ y = − x − 3
Ta lập bảng:
Hàm số y = − x − 3 đi qua hai điểm M(0; −3) và N(−3; 0).
b) (d) cắt trục tung tại điểm có tung độ bằng 1
Þ 1 = (m − 1).0 + m − 3
Û 1 = m − 3
Û m = 4.
Vậy m = 4 thì (d) cắt trục tung tại điểm có tung độ bằng 1.
c) Vì A là giao điểm của (d) với trục Ox nên yA = 0.
Khi đó (m − 1)xA + m − 3 = 0
\[ \Leftrightarrow {x_A} = - \frac{{m - 3}}{{m - 1}}\]
\( \Rightarrow OA = \left| { - \frac{{m - 3}}{{m - 1}}} \right|\;\left( {m \ne 1} \right)\)
B là giao điểm của (d) vưới trục Oy nên xB = 0
Khi đó yB = (m − 1).0 + m − 3 = m − 3
\[ \Rightarrow OB = \left| {m - 3} \right|\]
Để tam giác OAB cân tại O thì OA = OB
\[ \Leftrightarrow \left| { - \frac{{m - 3}}{{m - 1}}} \right| = \left| {m - 3} \right|\]
+) TH1:
\[ - \frac{{m - 3}}{{m - 1}} = m - 3\]
\( \Rightarrow \left( {m - 3} \right)\left( {m - 1} \right) = - \left( {m - 3} \right)\)
\[ \Leftrightarrow \left( {m - 3} \right)\left( {m - 1} \right) + \left( {m - 3} \right) = 0\]
Û m(m − 3) = 0
\[ \Rightarrow \left[ \begin{array}{l}m = 0\;\left( {TM} \right)\\m = 3\;\left( {TM} \right)\end{array} \right.\]
+) TH2:
\[ - \frac{{m - 3}}{{m - 1}} = - \left( {m - 3} \right)\]
\( \Rightarrow \left( {m - 3} \right)\left( {m - 1} \right) = \left( {m - 3} \right)\)
\[ \Leftrightarrow \left( {m - 3} \right)\left( {m - 1} \right) - \left( {m - 3} \right) = 0\]
Û (m − 2)(m − 3) = 0
\[ \Rightarrow \left[ \begin{array}{l}m = 2\;\left( {TM} \right)\\m = 3\;\left( {TM} \right)\end{array} \right.\]
Vậy các giá trị của m thỏa mãn là m = 1; m = 2; m = 3.

