Cho hàm số bậc nhất y = (m − 1)x + 4 có đồ thị là đường thẳng (d) (m là tham số và m ≠ 1).

a) Vẽ đồ thị khi m = 2.

b) Với giá trị nào của m thì đường thẳng (d) song song với đường thẳng y = −3x + 2 (d₁).

c) Tìm m để đường thẳng (d) cắt trục Ox, Oy lần lượt tại hai điểm A, B sao cho diện tích tam giác OAB bằng 2.

Lời giải

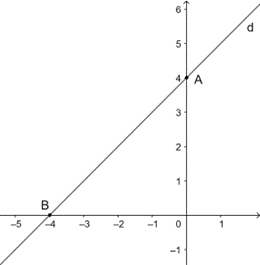
a) Với m = 2 Þ y = x + 4 (d).

Với x = 0 Þ y = 4. Suy ra đồ thị đi qua điểm có tọa độ (0; 4).

Với y = 0 Þ x = −4. Suy ra đồ thị đi qua điểm có tọa độ (−4; 0).

b) Để (d) song song với đồ thị hàm số y = −3x + 2 (d₁)

Þ m − 1 = −3 Û m = −2

Vậy m = −2 là giá của m thỏa mãn.

c) Đường thẳng (d) cắt trục Ox tại điểm có hoành độ \(x = \frac{4}{{1 - m}}\)

\( \Rightarrow A\,\left( {\frac{4}{{1 - m}};\;0} \right)\) Þ \(OA = \left| {\frac{4}{{1 - m}}} \right|\).

Đường thẳng (d) cắt trục Oy tại điểm có tung độ y = 4

Þ B(0; 4) Þ OB = 4.

Khi đó diện tích của tam giác OAB là:

\[{S_{OAB}} = \frac{1}{2}OA.OB = \frac{1}{2}.\left| {\frac{4}{{1 - m}}} \right|.4 = \frac{8}{{\left| {1 - m} \right|}} = 2\]

Û |1 − m| = 4

\( \Rightarrow \left[ \begin{array}{l}1 - m = 4\\1 - m = - 4\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m = - 3\\m = 5\end{array} \right.\).

Vậy m = −3 và m = 5 là giá trị cần tìm thỏa mãn của tham số m.