Lời giải:

Đáp án B

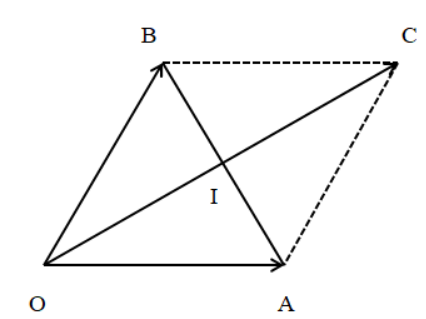
Đặt \[\overrightarrow {{F_1}} = \overrightarrow {OA} \] và \[\overrightarrow {{F_2}} = \overrightarrow {OB} \]. Khi đó ta có \[\left| {\overrightarrow {OA} } \right| = \left| {\overrightarrow {OB} } \right| = 50\,\,(N)\] và \[\widehat {AOB} = 60^\circ \].

Dựng điểm C sao cho tứ giác OACB là hình bình hành.

Theo quy tắc hình bình hành, ta có: \[\overrightarrow {OA} + \overrightarrow {OB} = \overrightarrow {OC} \] hay \[\overrightarrow {{F_1}} + \overrightarrow {{F_2}} = \overrightarrow {OC} \]

Suy ra lực tổng hợp của hai lực \[\overrightarrow {{F_1}} \] và \[\overrightarrow {{F_2}} \] là \[\overrightarrow {OC} \].

Do đó cường độ tổng hợp lực của hai lực \[\overrightarrow {{F_1}} \] và \[\overrightarrow {{F_2}} \] là \[\left| {\overrightarrow {OC} } \right|\]= OC.

Vì OA = OB và \[\widehat {AOB} = 60^\circ \] nên tam giác OAB đều, do đó: AB = OA = OB = 50.

Gọi I là giao điểm của OC và AB

⇒ I là trung điểm OC và AB ⇒ BI = \[\frac{{AB}}{2} = \frac{{\left| {\overrightarrow {AB} } \right|}}{2} = \frac{{50}}{2}\]= 25(N).

Tam giác OAB đều có OI là đường trung tuyến.

Suy ra OI cũng là đường cao của tam giác OAB.

Tam giác OBI vuông tại I: \[O{I^2} = O{B^2} - B{I^2}\] (Định lý Pytago)

\[ \Leftrightarrow O{I^2} = {50^2} - {25^2} = 1875\]

\[ \Rightarrow OI = 25\sqrt 3 (N)\]

Do đó OC = 2OI = \[50\sqrt 3 \] (N).